PROGRAM ASPECTS

Chapter 11. A mathematical model of the electrical activity in the heart and a simulation of an electrocardiogram: the computer simulation program HEART

This chapter discusses:

• a case studies about the electrical activity in the heart and the origin of the electrocardiagram (ECG);
• some aspects of neuronal networks;
• the behaviour of a large number of coupled oscillators and some basic electro-physiological principles.

Introduction

The educational aim of this program is not to teach students details which are necessary to be able to use the electrocardiogram as a diagnostic appliance. That is a real problem even for a well-trained cardiologist. This computer simulation program HEART shows students how an intricate phenomenon can be constructed with the help of modelling and simulation, i.c. the electrocardiogram, from underlying electrophysiological principles.

The interest nowadays for this kind of model divided into a large number of segments which are tested, lies in the current research about artificial neural networks with thousands of these segments.

History of models of electrocardiograms

In 1952 Hodgkin and Huxley described the electric activity in one nerve with a system of 4 differential equations (Hodgkin and Huxley, 1952). Until now it was apparently very difficult to describe a model at cell level for the total electrical activity and particularly the externally measured electrocardiogram of the heart, because of problems with the complexity. In literature models are decribed with a large number of cells with a simple cell model as their basis and models with the complete Hodgkin Huxley equation ('HH equation') in which perforce the number of cells is limited.

Even if good modelling of the electric sources were possible at cell level for the benefit of the ECG it could not possibly describe a complete ECG. The number of myocardiac cells that is involved (some 10 billion) is too large to include them all separately in the calculation . The model of the computer simulation program HEART was designed on a theory  by Rosenberg (1972) in which the (heart) segments each represent a quantity of myocardiac cells which can be described in terms of one single myocardiac cell and not in terms of Hodgkin and Huxley's model. The concept of Rosenberg's model and four experimental segment models have been the basis for the model by Min, Sparreboom and Kingma (1975). They  experimented at the University of Delft and the Erasmus University in Rotterdam for segments with the BVP and 'S' (Sarna) equations and designed electrocardiogram models with the help of the 'K' (Kingma) and the 'M' (Min) equations  (Sarna et al., 1972; Min, 1975). In 1982 this work resulted in the first version of HEART at the University of Limburg, and later on in the computer simulation program HEART at the University of Twente.

The total electrical activity of a segment can be described by such a system of mathematical equations ('lumped model').

After 1975 others proceeded with the models of Min, Sparreboom and Kingma. Ten Have continued with the models and improved the method of coupling (Ten Have, 1975). Van den Heuvel introduced more details to the heart model of Min, Sparreboom and Kingma, particularly the possibility of simulating a more realistic shape of the electrocardiogram during arhythms and heart blocks. (Van den Heuvel, 1976).

Segments
The division of segments of the heart has been chosen in such a way that the average of the intensity and the direction of all electrical activity is just as in the humen heart so that it can simulate an electrocardiogram of the waves. The BVP as well as the HH, the S, the K and the M equations meet the requirements to enable the simulation of such a segment. These differential equations all have a periodical solution and are therefore autonomously oscillating. Such an equation or such a segment is conceived as an oscillator. All these equations also meet the requirement that under certain conditions there is no periodical solution but they can be tiggered by another segment. Thus electric activity of pacemaker tissue, conductive tissue and also myocardiac cells can be simulated with these equations. In the model of the electrocardiogram there are a few segments of the spontaneously oscillating type and others of the kind that can be triggered.

A segment represents a group of myocardiac cells whose electromagnetic field runs more or less in the same direction. Or to put it differently: the heart is divided into segments so that one segment is characterized by the resultant of all electromagnetic fields and an average of activation and deactivation moments of the separate cells.

The model by Rosenberg et al. has 13 segments. Rosenberg describes that the externally measurable electric activity, the electrocardiogram, can in all its leads, be derived from the electric activity of the segments separately. The quantity of cells which a cell represents in reality and the direction coefficient of the resultant of the electromagnetic field of a segment is of the utmost importance here, by means of a method of weighing factors in relation to conduction. Rosenberg deducts the externally measurable electric activity, the electrocardiogram, from the separate electric activity of the segments.

Figure 11.1. The 14 segments of myocardiac tissue in the block diagram of the model of the heart in the computer simulation program HEART (Rosenberg et al., 1972; Min, 1975).

The HH, BVP, S, K and M equations

the HH equations
The general equations Hodgkin and Huxley gave to the system of non-linear differential equations in 1952 describing the cell membrane activity are:

dV/dt = ( GNa.m2.h.(V-VNa) + GK.n4.(V-VK) + GCl.(V-VCl) + Ii ) / C
dm/dt = am.(1-m) - bm.m = f(m,V)
dn/dt = an.(1-n) - bn.n = f(n,V)
dh/dt = ah.(1-h) - bh.h = f(h,V)

with V, the membrane potential; Ii the membrane input activity; GNa, GK and GCl are the conductivity for sodium, potassium and chlorine ions respectively; VNa, VK and VCl are constants; C the membrane capacity; m, n and h are auxiliary variables for sodium, potassium and chlorine respectively. This system of equations is called the Hodgkin Huxley (HH) equations.

the BVP equations
Many authors have tried to find a system of equations of a lower order. The 'HH equations' are 4th order non-linear differential equations in which a relatively large complexity is rapidly created by the forming of cascades of cells, the elements: Fitzhugh (1961), Linkens and Mohne (1979), Van Capelle et al. (1980). The 'BVP equation' is a good substitute for the 'HH equation' and a good model for electric activity of a group of cells. Firstly because the system of equations has under certain conditions a stable periodical solution as well as a stable 'singular point' (steady state) at which after a trigger signal periodical solutions are possible. And secondly because with the calculation this equation is less laborious than the relatively complex HH equation. A weighty argument in extensive models on cell basis, because of the quantity of cells per volume unit in a segment of an organ. The system with the two first order differential equations by Bonhoeffer and Van der Pol are:

dx/dt = c (y + x - x3/3 + Ip)
dy/dt = - (x + a + b.y) / c

with a, b and c as constants. Ip is the input signal if this segment is coupled to another. These equations are called the 'BVP equations'.

the S equations
Sarna and Kingma extended this system to:

dx/dt = k (a1.y + a2.x + a3.x2 + a4.x3) + Is
dy/dt = - (b1.y + b2.x + b3.x2 + b4.x3 - b0) / k + Is0

with a1 until b4 constant. Is and Is0 are the input signals if this segment is coupled to another. These equations are called the 'S equations'.

the K equations
Kingma proposed a variant which contained not only a simple non-linear part but economized in analogue as well as in numerical methods of solution. It looks like this:

dx/dt = a1.y + a2.x + a3.F(dx,cy) + Ik
dy/dt = b1.y + b2.x + b3.F(dx,cy) + Ik0

with a1 until b3 constant. Ik and Ik0 are the input signals if this segment is coupled to another. F(x,y) is a non-linear function. These equations are called the 'K equations'.

the M equations
In order to be able to compare all these equations mutually in theory it is necessary to bring the equations in the form x = y - F(x) and y = g(x) to explain their similarity in periodicity and ability to be triggered, according to Min, Sparreboom and Kingma. These insights produce the equations:

dx/dt = a.y - b.x + c.M(x) + Im
dy/dt = - d.y - e.M(x) + Im0

with a, b, c, d and e as constants. Im and Im0 are the input signals if this segment is coupled to another. x is the total electrical activity in this type of segment. M(x) is a specially designed non-linear function of x according to theories of Lienard. These equations are called the 'M equations' (Min, 1975).

Figure 11.2. In this schematic drawing of the electrocardiogram is indicated where separate segments play a part in the realization of the electrocardiogram. The state of activation of a segment is indicated with a horizontally drawn line and during the period of inactivity of the segment no line is drawn.
On the right of these lines are the values indicated of the weighfactors. The positive value indicates a rise and a negative value a fall in the activity of the ECG. The indication f5 to f13 indicates that the simulated electric activity of a segment has been subject to a shape correction of the signal in the model.

Each segment of the model of the electrocardiogram has its specific characteristics like active (autonomously oscillating) or passive (not autonomously oscillating), an activation and de-activation moment, a certain length of the activation period and the shape of the electric activity agreeing with the sum of all action potentials of the cells in a segment, defined by the constants and values of the non-linear elements such as F(x) and M(x). The ECG finally comes about by the sum of the electric activity by means of the method of Rosenberg as described above.

The model of the electrocardiogram

Figure 11.3. The normal 'healthy' electrocardiogram as it can be simulated with the computer simulation program HEART. Here the electric activity of 7 segments is simulated. The order of the activation of the segments can be seen clearly (VL3 speeds on with respect to VL2, VL2 speeds on with regard to VL1, etc.).
In the 'steady state' situation there is a stable QRS complex and a P and T top. The ST interval, the 'flat' part in the ECG between the S top and T top, has a difference in potential of O mV at the moment that left and right ventricles both fire.

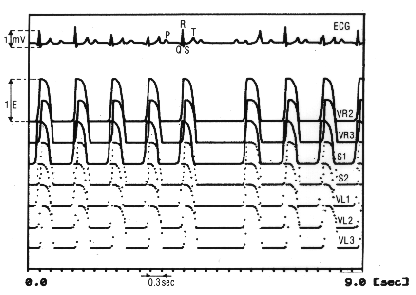
The A-V segment plays a role in the conduction of the atrial activity to the ventricles. The segments SA, VR1, VR2, S1, VL1, VL2, VL3 are autonomously oscillating actively. The segments called AR, AL, HIS, VR3, S2, VL4 are passively, not autonomously oscillating and are therefore dependent on activation by neighboring segments. The A-V segment consists of an active and a passive element. The model counts beside the excitable elements also 8 correction elements.

Figure 11.2 shows the periods of the activation (drawn line) and the 'non activation' in the 12 segments of the myocardiac tissue of this model. In this figure the weighing or conductivity factors are also indicated representing the contribution of each heart segment separately in the electrocardiogram. By simulating the disturbances in conduction between atrial and ventricle, arhythms can arise in this model.

The model of the computer simulation  program HEART is written in Fortran and implemented in the RLCS system of the University of Limburg and runs on PDP 11 computers and on VAX computers (VMS) with at least one Tektronix terminal.

Figure 11.4. An electrocardiogram (ECG), simulated with the 'K equations' and the model of the computer simulation program HEART, implemented in the RLCS system. A characteristic Wenckenbach cycle has been simulated by decreasing the conductivity between atrium and ventricle, one of the intervention parameters of the model. The amplitudes of R and T top are not meant to be realistic, which is clearly illustrated by the first QRS complex and T top after the blocked P top.

Results

Discussion

Note
This chapter is corrected summary of an un-published chapter of the Ph. D. thesis of Min (1982). Because the discussion now a day about neuronal networks this chapter is inserted here.