LEARNING ASPECTS
Chapter 1. Computer simulation as a cognitive tool and learning object
This chapter discusses the following issues:
Computer simulation for educational purposes is a part of what is called computer assisted learning (CAL). Sometime the term computer assisted instruction (CAI) or computer based training (CBT) is used. Nowadays the term multimedia is often used in stead of CAI, CAL or CBT because all educational software looks like regular multimedia products. Computer simulation is one of the eight classical forms of CBT, CAI or CAL situations. For computer simulations we prefer the word 'computer assisted learning' (CAL) instead of the American word 'computer assisted instruction' (CAI) because of it's focus on learning instead of instruction. Computer simulation as learning concept is situated in an open, exploratory setting. Open learning environments based on our concepts are, in fact perfect examples of multimedia.
1.1 Computer simulation and modelling
Computer simulation is a form of learning with computers in which the user may experiment with a simulated situation. This situation strongly resembles reality or is a deliberate simplification.
Computer simulation enables students to make decisions without running great risks. As a result of the decisions made the computer reacts with informative feedback. This feedback is almost always of a visual nature. Visual feedback is an important characteristic of computer simulation. Therefore a computer simulation program often has the characteristics of an animation program. Computer simulation programs are multi-media programs.
Computer simulation in the instructional situation offers the teacher the possibility to provide experimentation with the subject matter in an ordered way. Moreover it can make it easier to realise goals set beforehand.
There are many definitions of computer simulation. Unfortunately many authors do not make a distinction between simulation and modelling. A number of definitions from literature illustrate this:
Hinton, 1978: 'A simulation package is based on a known model of physical phenomena. The model, usually in the form of a mathematical relationship, can be set up within a computer program and the student can simulate the phenomena or process by controlling and observing the output.'
MacArthur, 1984: 'A simulation is simply a model of some aspects of reality to focus on points of interest.'
Manning and Potter, 1984: 'The objective of simulation models is to present a simplified version of reality, whereby a complex system is distilled to only its most important elements or variables.'
Shaw, 1984: 'A computer simulation is a simplified representation of a real event or thing that recreates pertinent characteristics.'
All these definitions are incomplete in view of the perspective of this chapter and the classifications used. Hinton's is the most complete. MacArthur does not make a clear distinction between a simulation and a model. His definition would have been more correct if it had said: 'A simulation is simply based on a model'. Neither is Shaw precise in his distinction of the model as opposed to simulation, for a simulation is not a representation: a model is a representation and with a model simulation becomes possible.
It must be stressed, as many other authors have noted that in the field of computer-assisted learning a distinction has to be made between simulation and modelling. Hinton for instance, says this:
'In the area of computer-assisted learning it is useful to make an operational distinction between simulation and modelling. It will be assumed that a simulation allows the student to control input parameters and to observe the output. The model, usually in the form of a mathematical relationship, is set up within the computer program and the student can simulate the phenomena or process by controlling the input and observing the output. In modelling the student is able to control or change the model upon which the simulation is based.'
| DEFINITION: Computer simulation is a simulation environment on a computer screen. Most of the times based on a mathematical model. Sometimes also combined with a knowledge or rule-based system.
|
The student learns to change the model and its relations until the model concurs with the mental model the student has in mind. (See figure 1.1.)
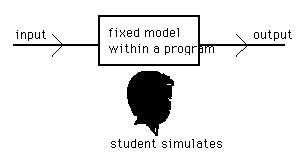
Figure 1.1 The process of computer simulation represented schematically: the student is learning something about relations between interventions and variables with a simulation program based on a fixed model.
There are a number of definitions of computer simulation in teaching. We seldom find a universally accepted definition in literature. Frequently, this is because a distinction between simulation and modelling as separate forms is rarely made, as has been demonstrated here.
| REMARK: Simulation and modelling are important forms of CAL or CBT or educational multimedia programs for learning.
|
In computer assisted learning situations, modelling is 'learning making models or conceptual models' (as showed in figure 1.2) and simulation is 'learning relations with fixed models'.
Classification of computers in education:
The classification of the use of the computer in education, concerning CAI or multimedia is more or less a traditional classification.
The computer on school varies from word processing, where the computer is used as an complex instrument for professionals, until 'simulation CAL', where the computer is used as a 'simple in use' learning machine for children and students. There are 4 classes and a lot of sub-classes of use of the computer in education:
Instrument
The computer as an instrument (particularly for the staff):
Object
The computer as an object of study:
Help tool
Learning with the help of the computer computer and images support the instruction, as a help tool in education:
Learning environment
Environments for learning (CAL) or instruction (CAI):
This American/English classification: drill and practice, tutorial, dialogue, inquiry, simulation, modelling, gaming and problem solving still plays an important role, because each multimedia program is a mixture of these forms. This can be essential for an analysis of a program. For example, to be able to weigh up the didactic advantages against the disadvantages.
Tutorial courseware is typical computer assisted instruction (CAI) and simulation courseware is computer assisted learning (CAL).
|
The use of simulation languages in order to test or make models has to be regarded as computer supported instruction. The mere drawing of graphs does not necessarily have anything to do with simulation and is just using the computer as a tool.
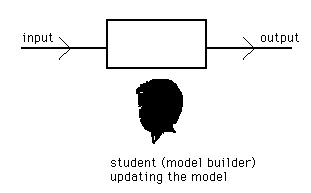
Figure 1.2 The process of modelling represented schematically: the student is learning modelling by making models - or parts of it - in a modelling system.
Computer Simulation
It is necessary to attempt to define the concept 'computer simulation', since in the literature anything in which a computer is used to simulate something, is called computer simulation. A definition of computer simulation which is too vague or inexact will lead to misunderstanding in e.g. a discussion of specific advantages of computer simulation. The following question for instance, requires a common understanding of what is meant by simulation:
'Can a simulation in the form of an inquiry CAL-program, in which the student has to think up and pose questions, also be used as a simulation of a certain phenomenon?'
It is necessary to distinguish at least four different kinds of computer simulation,
simulation of conversation
simulation of the behaviour of an expert
simulation with moving pictures.
simulation of phenomena (model-driven simulation)
each with its specific internal characteristics and not with typical graphical feedback in respect of its use as an educational tool. The last kind of simulation is the most important kind of simulation in the scope of this book. This kind of simulation is always based on a mathematical model.
Simulation of conversations
Conversation between man and computer e.g. the physician-patient conversation, involving 'history taking', is 'simulation of conversation'. This kind of simulation is classified in this chapter as 'inquiry CAL', because the user ask or search a question to the simulation program. Examples of this are programs by Verbeek (1986) and the training program by Min and Ephraim (1979: ANAMNESE) and Van Oenen (1989: MacCOAT). (See chapter 14.)
The student has to be able to ask a series of questions with a minimum of coaching. The simulated 'patient' answers the questions of the (medical) student, the 'prospective physician'. Below there is an example of such a simulated conversation from the ANAMNESE program. On the screen a list of questions appears:
1. Do you suffer from listlessness?
2. Do you suffer from fatigue?
3. Do you suffer from pain in your chest?
4. Does the pain radiate to your arms?
The student chooses one or more questions and receives an answer from the simulated patient after having typed in the numbers of the questions,
3. No, I do not suffer from pain in my chest.
1. Yes, I have been feeling listless for the past few weeks.
Simulation of the behaviour of an expert
In this form of computer simulation a mathematically described model is not the 'nucleus' of the computer simulation program but an expert system or a knowledge base instead. This form is usually called 'intelligent CAL' or CAI and often abbreviated to ICAI.
Expert systems are more and more assuming the role among the social sciences and particularly the medical sciences which mathematical models have played for a long time in physics. Both systems (models and expert systems) are based on rules and knowledge of experts that can be used by a third party such as the student.
An example of a computer simulation of an expert gives the program PHYSICAN / ARTS. The simulated 'expert' answers after the student has introduced a great number of data. The fragment is from this program and works with conditional chances (see also chapter 14). On the screen appears:
Do you feel any pain while straining?
The student answers: YES. On the screen appears:
Do you feel pain on the middle of your breastbone?
The student answers: YES. On the screen appears:
Do your legs hurt?
The student answers: NO. etc. Finally the 'simulated expert' answers:
The most likely diagnosis, with a chance of 89%,
is to 'my' opinion: Angina Pectoris.
Simulation with moving pictures.
This kind of simulation with a large number of fragments of moving pictures which give the impression that each picture is unique, practically always occurs within the framework of ordinary 'tutorial CAL'. Programs with 'moving pictures' and 'highly visualized multiple choice moments' are most of the times 'tutorial CAL programs'. In the literature many programs labelled as simulation in fact turn out to be only tutorial CAL and are subject to all the disadvantages of tutorial CAL programs rather than enjoying the advantages of 'real 'simulation CAL' programs' (see chapter 2).
Simulation of phenomena (model-driven simulation)
Simulation of phenomena almost always involves phenomena that can be described with a mathematical model. In this book this is the most important kind of computer simulation. In this chapter this form is called 'real simulation' in the classical sense, here defined as: 'simulation CAL'.
| DEFINITION: Simulation CAL is courseware enabling a student to learn how reality works in his own hands.
|
This kind of computer simulation is a part of which is often called 'virtual reality'. But computer simulation and virtual reality is not really exactly the same. See the discussion in the literature.
The combination between mathematical models and expert systems is defined in this book as 'intelligent computer simulation' or ICS. In this book we avoid real 'intelligent computer simulation programs', so we prefer to use the words 'learning environments for simulation' or 'model-driven simulation'.
|
DEFINITION: Model-driven simulation is simulation based on a mathematical model
|
| DEFINITION: Intelligent (model-driven) simulation (ICS) is simulation based on a mathematical model combined with a rule- and knowledge base which monitor the output and the input of the simulation session.
|
Examples of this kind of simulation are the computer simulation programs CARDIO and FLUIDS. These programs are described later. An example of a simulated physiological process can be seen in the following fragment of the computer simulation program CARDIO using text instead of graphic display (chapter 9). The computer simulation program shows on the screen:
T=0 hour; mean arterial pressure: 100 mmHg.
etc.
To enable the student to intervene in the process the following questions appear on the screen:
Which intervention do you want to do?
1. Contraction strength heart muscle
2. Renal arterial constriction
3. Vasoconstriction
The student chooses 1. On the screen appears:
This parameter is now fixed at 1.0 units.
How many units do you want?
The students types: 0.4. The program proceeds with:
T=1 hour; mean arterial pressure: 75 mmHg.
'Doctor, I feel so dizzy'.
T=6 hours; mean arterial pressure 80 mmHg.
'Doctor, my shoes pinch, my feet are swollen'.
In this chapter experimenting generally means the single or multiple changing of model parameters or starting values of variables, also called 'intervention in the model', in order to study the reactions. To illustrate this kind of simulation (simulation of phenomena), a simple system with three water tanks is represented in figure 1.3 .
Taps 1 and 2 are here the intervention possibilities, the model parameters. At the same time it is a combination of a visually designed conceptual model and an animated representation. By changing the parameters, opening and closing the taps, the student can note changes in the dynamics of water levels. The water levels are the dependent variables of this model. So the student experiments with a representation of reality and not with reality itself. By visualising and representing the dynamic behaviour in this way experiments are possible without mathematical knowledge or simulation languages.
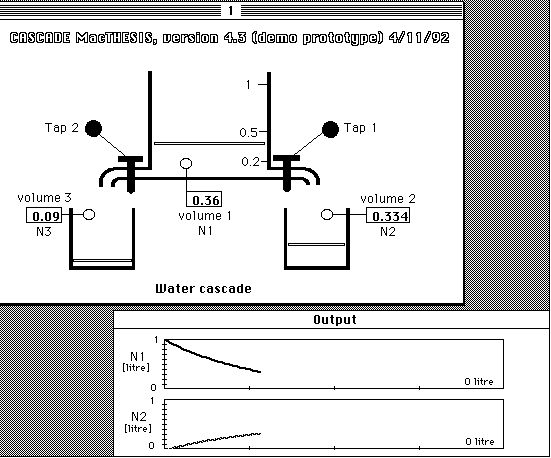
Figure 1.3. Model-driven animation in a computer simulation program based a model with three moving water levels and a turning pointer. Taps 1 and 2 are the intervention possibilities in this model. The underlying model recurs in concept at various places in physics, chemistry and biology. In this program these principles are explained with the help of a water cascade as analogon. (Computer simulation program CASCADE; MacTHESIS system).
Another example of a computer simulation program, frequently described by Wedekind (1981) and other biologists, is of two populations living in the vicinity of grassland, viz. hares which eat grass and foxes which in turn eat hares (see figure 1.4). The interaction can be recorded mathematically by two differential equations, the so-called Lotka-Volterra equations:
For beasts of prey:
dNr/dt = br.Nr - dr.Nr.Nb - Nr/k
For prey:
dNb/dt = bb.Nb.Nr - db.Nb
in which N, b, d and k are the model parameters. And further:
Nb the quantity of prey (game, e.g. hares)
Nr the quantity of beasts of prey (e.g. foxes)
br the 'birthrate' of beasts of prey
bb the 'birthrate' of the prey
dr the 'death-rate' of the beasts of prey
db the 'death-rate' of the prey
k the factor relating to the 'quality of the environment'.
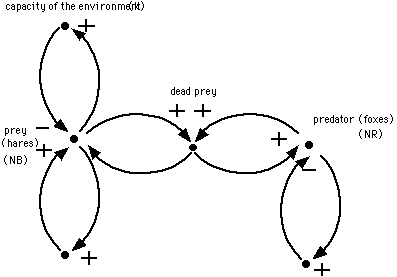
Figure 1.4 Interaction diagram of the classic prey-beast of prey model.
When the student changes the values of these model parameters, he or she can observe the results of these changes on the screen. In a program like this, with a model that is often used as an example of a computer simulation program, there has been a great deal of experimentation with various forms of representation. These forms varied from simple numerical designs to all sorts of animated representation an example of which is shown in figure 1.5.
Computer simulation programs based on mathematical models should be designed in such a way that the student can easily use and intervene in the model, visualized in the first page or window of the program. The output of a 'simulation run' is mostly shown graphically or with some kinds of animations on a second or a third page or window.
The model with the marked locations for intervention and most of the output aspects can be represented visually - as much as possible - as can be seen in figure 1.3 (CASCADE), figure 1.5 (ECOLOGY / LEMMING), figure 1.8 (CARDIO) and figure 1.10 (BRINE PURIFICATION / PEKEL).
A parameter can be changed by using a mouse and clicking in an 'in click region'. This form of intervention in a computer simulation program is here called input-animation-technique. Programs using this technique will be discussed in later chapters. An example is given in figure 1.8. Computer simulation programs made with the design system MacTHESIS apply this technique, enabling the simulation programs to have the character of a real educational appliance instead of merely a computer with a keyboard.

Figure 1.5 A 'co-moving' histogram graphic represents action of a model from ecology. In this screen the relations existing between a population beasts of prey and a prey population are given. By changing the parameters death rate and birth rate, the mutual influence of the populations can be studied. (computer simulation program LEMMING, MacTHESIS system).
DEFINITIONS: Simulation CAL versus tutorial CAI
Much of what is called computer simulation is in fact 'tutorial CAI', such educational software is called quasi computer simulation. Figure 1.6 shows the structure of 'tutorial CAI'. At a moment of decision the program determines on the basis of the choice of the student which frame(s) (the smallest possible representation units) are presented subsequently. Moments of decision can be anywhere. Frames with moments of decision are here called acceptation frames.
Texts, graphs or animation are in so-called presentation frames. When there is a computer simulation program in a presentation frame of a tutorial structure this CAI lesson has become a 'simulation CAL' program, (see figure 1.7). The characteristic structure of 'simulation CAL' is that at a moment of decision the decision is taken by the underlying (mathematical) model in the last instance and so indirectly by the pupil. On the other hand, the pupil determines initially the intervention in the model. 'Simulation CAL' is therefore pre-eminently student controlled, but the progress in a lesson - the choice of the following series of presentation frames - is determined by something else than just the student.
A second confusing aspect is the problem that an educational program with movement, animation or video pictures, is often called simulation while it is in fact 'tutorial CAI'. When the series of presentation frames is very large, for example more than a thousand possible supplementary presentation frames, then it can happen that a designer calls his program a simulation program. This is not correct in view of what was said above about a model which has to underlie a simulation or that the animation is not interactive, but simply sequential.
Tutorial CAI behaves didactically different from other computer simulations with a model of a system from reality. So the advantages of the one form of simulation are not always equal to the advantages of the other form of simulation. Tutorial CAI is computer controlled and 'real' computer simulation is student controlled. The student has to ask himself questions and draw up and test hypotheses and should continually take the initiative.
'Real' simulation CAL is characterised by the fact that it can take an unlimited number of positions. Each decision of a student gets a unique response. The visual feedback is different for each student. A single change on a parameter of a model is not reproducible, let alone the model-response and the value of a certain variable which eventually determines which picture fragment is presented (see figure 2.8). So in 'real' simulation CAL each student-session produces a non-reproducible (unique) series of pictures.
END DEFINITIONS
|
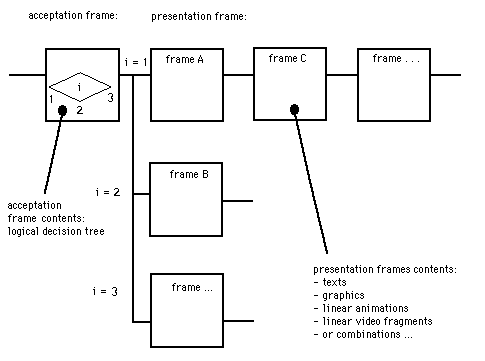
Figure 1.6 'Tutorial CAI' with frames and a menu-frame. The structure characteristic is the clear moment of decision. In the so-called 'acceptation frame' the answer could be 1, 2 or 3 but nothing else. After an answer the lesson continues. The other frames (of the lesson) can be any kind of CAI or CAL.
Modelling
In addition to simulation, modelling is one of the eight forms of CAL, at least according to the 'traditional classification' used in this book. Modelling is distinguished from simulation in that the student develops a model on his own which represents a situation in reality. The model itself in this form of CAL is continually subject to discussion and is not regarded as a fact as occurs in simulation. Modelling aims to develop the ability to systemize complex relations within a system. Modelling involves executing certain
purpose tasks in order to record the inter-relationships within a certain system. This happens in two steps:
definition of a system from reality,
representation of this system in a model.
Modelling involves learning to make a model of something, such as making a mathematical model, drawing a flower in LOGO, or making a program for a 'programmable logical controller' (PLC) that resembles a robot. Programming in its widest sense is also included here as modelling in this book. (See figure 1.9.)
| DEFINITION: modelling CAL is courseware enabling a student to learn how models can be made.
|
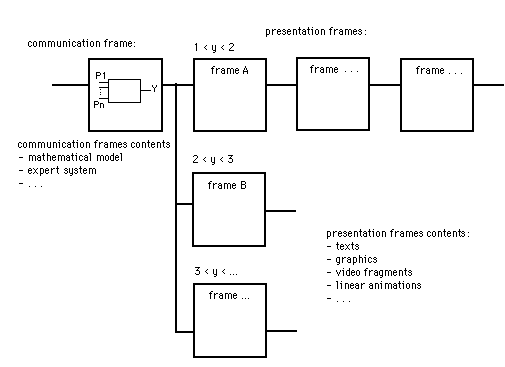
Figure 1.7. 'Simulation CAL'. Primary characteristic in this kind of courseware is that the moment of decision has a series of ranges. The decision to choose a presentation frame depends on the reaction of the (mathematical) model. When a certain output variable (here y) lies between two values (for example between 1 and 2, or 99 and 100), then the second or third branch is chosen, etc. The next frames can be any kind of courseware: tests (CAT), tutorial or inquiry CAI.
Simulation in contrast, involves learning to experiment with a simulated reality. Although models are used while doing this, the simulation programs are 'discovery environments' aiming to transport reality into the classroom. The student trains or does exercises while learning to see connections between quantities and components of a system.
An example is a simulation of the Dutch economy. Its purpose is not to make a model of the Dutch economy but to gain an insight into how this model is built up.
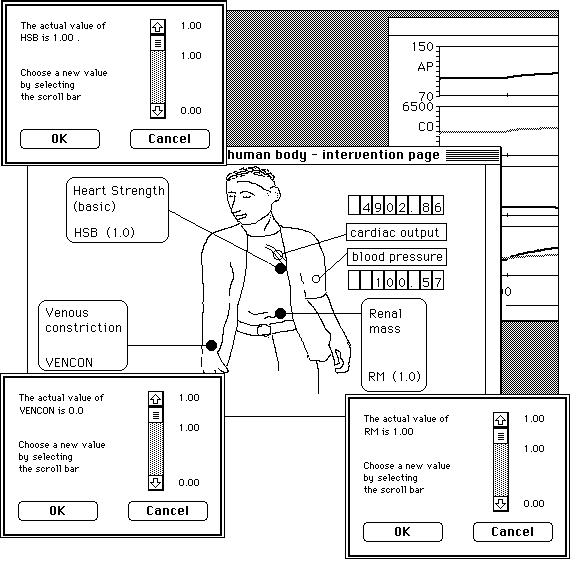
Figure 1.8. An example of 'input-animation technique'. This program consists of two windows: the animation window and the representation or output window. These windows can be placed one on the other, but also next to each other. (In Macintosh terms this is called 'desk top'). In the animation window there are 'click-in regions' by which an auxiliary window with a scroll bar it can be whipped up. With this scroll bar a parameter of an underlying model can be adjusted. (computer simulation program CARDIO, MacTHESIS system).
It sounds paradoxical but computer simulation programs turn out to be very useful in higher education or industrial training for learning how to make a model. For example a computer simulation program of the blood pressure regulation mechanism of the human body (CARDIO or FLUIDS), enables a medical student to construct a (conceptual) model of the relation between blood pressure, cardiac output, and peripheral resistance and to find that they are linear.
1.2. Reality, system, model and program
The educational use of simulation aims to develop in the user a feeling for the relationships between different variables of a model. However, this feeling cannot be verified because it cannot be put into the computer and can therefore never be made quite clear. It is even doubtful whether every user develops this feeling at all. Moreover not all relations are recognized by the user, because the designer may have had to simplify the program. Beside certain important elements are difficult to represent in a mathematical model, so that these elements cannot be transposed into a computer simulation program. Too much attention might then be paid to matters which can easily be condensed into a model and which are (educationally speaking) of very little or no importance .
It has been found that in computer simulation purposeful actions are executed with a model fed into the computer. With 'gaming' it is also calculated and displayed how the set aim is achieved. The model is here a substitute for a phenomenon or event from reality. Instead of the terms 'event', 'phenomenon', or 'reality', the general term 'system' can be used. Now we shall try to explain the relation and differences between reality, a system, a model and a computer simulation program.
Figure 1.9. A simulation program for secondary and technical education to simulate a 'programmable logical controller' (PLC) and the PLC language (Wolters, 1986). The part of learning how to program the PLC is the modelling part, because the student makes a program to control a technical installation. ('Simulation CAL' combined with 'modelling CAL' in one 'simulation program')
The 'really existing' system
A system is defined as the connection of parts in an existing reality, which are related in a certain way to each other, to the whole and to their surroundings, and which interact and influence each other. Kornbluht and Little (1976) say about this:
'A system means a grouping of parts operating together for a common purpose. An automobile is a system of components that work together to provide transportation.'
Another example of a rather complex system is our national economy. The separate components of the economy influence each other in the production, distribution and consumption of goods and services.
According to Kornbluht and Little, a number of specific characteristics are connected with the term system. The most important of these is the state of the system. This state is related to the value or state of the parts of the system at a certain moment. In some cases this state can vary from time to time, in others it remains (practically) stable.
A system is described as stable when the measured state varies only within an accepted margin, in spite of the occurrence of changes among the separate parts. If the measured state alters beyond the accepted margin the system is described as unstable.
If we want to examine a problem which is specifically related to a certain system, we first have to determine where the margins of the system are: what do we want to represent of the system in the model, and what not. Next we can try to make a representation of this system. This happens in the form of a model. The model can then be regarded as a substitute of the system. With the help of such a model it is possible to indicate the important and usually rather complex relations within the system.
The model
The construction of models representing a system is a complicated, specialized and labour intensive activity. That is why the production of computer simulation programs in education generally uses models which have already been developed for research in other disciplines. Modelling is most advanced within physics, chemistry, biology, and economics. So it is not surprising that we find most educational computer simulation programs within these disciplines.
A model is an abstraction of reality and can in fact be regarded as a substitute for the real-world system. The model is used to indicate the most important parts of the system and the (causal) relations within. However, it does not give a detailed, statistic description of a system, but it does show its dynamic character.
A number of models can be distinguished with which a real-world system can be represented:
Conceptual or mental model:
A conceptual model is an idea that a researcher has of the system which is being researched. A conceptual model usually precedes an empirical or mathematical model. Mental models are formed by experience, knowledge and intuition. In this chapter we don't describe and discuss gender aspects. The advantages of mental models are their possibility to be transmitted in conversations and the fact that the researcher can use his - or her - own creativity in working them out. Disadvantages: People can combine only a limited number of quantities in their minds (Miller: The magical number 7 plus or minus 2), long-term-predictions are verifiable on the short term and the mental model can behave in a rather unverifiable way. Moreover it is often only accessible for the person in question.
Empirical model:
An empirical model depicts the studied system somewhere else in the empirical reality, e.g. a scale model for a physics system or a game model for a social system. Through a scale model of the Delta works one can e.g. simulate a spring tide. Since an empirical model has come about by empirical research, it is as a rule more valid than a conceptual model.
Mathematical model:
By definition a mathematical model makes use of mathematical symbols in order to describe a system. These models have been used for this description because mathematical models have a number of specific characteristics:
mathematical models are very precise with regard to describing relations:
by mathematical formalization, logical contradictions are avoided;
it is possible to describe complex ideas and behaviour with relatively few symbols.
All kinds of mathematical models can be translated into a computer language without any particular difficulty by individuals experienced in designing computer simulation programs. For example: students of the University of Twente can do this after having completed a training with the MacTHESIS system. They are able to translate each kind of well-defined mathematical model to a Pascal source to implement it into the MacTHESIS simulation system. (See chapter 3.)
Kornbluht & Little (1976) discriminate another specific kind of mathematical model viz. simulation models: 'A special class of mathematical models referred to as simulation models. The term simulation refers to how the model is constructed. A simulation consists of the construction of a state (system) history previously defined as a succession of state (system) descriptions. A simulation often (but not always) employs mathematical symbols to represent the interaction of system components at different points in time. Thus simulation models are dynamic models. They involve changes in the state of the system through time. A simulation model expresses the dynamic relationships among the variables, constants and parameters.'
This is in fact the discussion with regard to models that are described in terms of analytical equations, which are often not interesting enough for computer simulation programs and which can simply be calculated with spreadsheet programs as opposed to models which will be discussed here and which are described in the form of differential comparisons, of which no analytical solution is known. Neither geometrical models are discussed here, nor calculation models.
The program
The ultimate goal of working with a computer simulation program is to acquire insight into a process or phenomenon, in short, in a system that is represented through a model in a computer simulation. One aspect of this goal is that the student tries to detect the structure, its being inter-connective, or the behaviour of the entity which is being simulated. This kind of discovery is made possible because the program enables students to vary parameter values in the model and to analyze the outcome of these variations. The benefits of these discovery experiences increase as the educational and technical aspects of computer simulation programs are enhanced.
With such computer simulation programs the student gets efficient and direct feedback from the program when he or she changes the model parameters.
This feedback is related to the consequences the input has on the underlying model. This feedback may be represented graphically, in tables, in animation form or in another form of representation, often also provided with some sort of comment. The student formulates a hypothesis which he or she tests and to which he or she gets an answer or material from which he or she may draw a conclusion. The correctness of the hypothesis is examined by intervening in the model and noting the results of the intervention. On the basis of these results, or other feedback, the student can adjust his hypothesis. This process of intervening and adjusting continues until a certain kind and level of insight in the simulated system has come about.
1.3 Computer simulation and learning
Introduction
Many advantages can be cited with respect to the use of computer simulation programs in education. A number of these do not specifically relate to simulation only but also to the validity for practical laboratories or the use of the computer in education in general. There are some specific advantages connected with computer simulation. First, some general advantageous aspects of simulation as a form and method of learning will be indicated.
* Computer simulation offers the opportunity to experiment with phenomena or events, which for a number of reasons, cannot normally be experimented with in the traditional way. Bork (1981) remarks: 'Simulations provide students with experience that may be difficult or impossible to obtain in every day life'.
In class it is e.g. not possible to experiment actively with an economic system. The only thing the teacher can do is to discuss the nature and content of the system. Experimenting would surely be useful because this can generate an insight into the functioning of the economic system.
* Computer simulation Programs can be used in education to give the student more feeling for reality in some abstract fields of learning. Foster (1984) says about this: 'Simulations can be entertaining because of dramatic and game-like components'.
* When a teacher tries to explain a difficult interrelationship, such as a hybridization experiment with fruit flies in the traditional way it is likely that part of the class will fail to understand. Execution of the real experiment is impossible because this would take a number of weeks and can therefore not be integrated as such within a lesson. When, after the necessary theoretical discussion of the material, a simulation experiment follows there will be a greater chance that more students will understand a complete relationship, such as a hybridization experiment.
According to Elron (1983) the best simulation does not have to resemble reality in the most accurate way. The power of simulation often lies, according to him, in the simplification of reality. Good simplifications provide students with a better insight into reality than by examining all components of a complex situation.
While working with a computer simulation program the student is experimenting, so he or she is playing an active rather than a passive role. This active engagement contrasts with the situation students often experience during 'face-to-face' teaching when they listen passively. Simulation creates, according to Foster, an interactive educational setting which offers the possibility to effect changes in relation to the learning experience in a more efficient way than is normally possible with other didactic methods.
It is obvious that computer simulation does not work to its intended advantage on face-to-face teaching (lecture type). Nor does it stand alone. Only when computer simulation is appropriately alternated with other didactic forms, will it render a positive result. Working with a computer simulation program often evokes enthusiasm in the student and as such it has a positive influence on his motivation. Spitzer remarks on this:
'Simulations are highly motivating, both intrinsically and extrinsically.'
However, no educational tool is effective for everyone. A differentiated supply of educational support tools is therefore important. A computer simulation program is one of them.
Working with a computer simulation program can increase the interest of a student about a subject. This can express itself in the fact that students will often study relevant literature concerning the subject after using a simulation more than they would have done with the traditional approaches to learning. The subject is discussed more among students and special experiences are mentioned.
The computer can be used as a didactic medium and in this form it can serve as a tool to realize a chosen educational strategy and to reach the set goals in a way that would otherwise have been impossible. But what justifies the use of computer simulation within the situation of the classroom? Which specific didactic functions can computer simulation fulfil in education?
Often the technical possibilities and the particularly effective calculating capacity of the computer are advanced in order to justify a switch to the use of computer simulations in classrooms. These reasons, according to Wedekind (1981), are not enough, especially from an educational point of view. The didactic functions that are possible with computer simulation are much more important.
Students are then offered the possibility to experiment with the real world system, though it is simulated. Computer simulation also offers the possibility to repeat the experiment as often as necessary, i.e. until the intended insight into the system has been acquired. It is also possible to do extreme things in computer simulation and to observe the results, contrary to many traditional experiments.
The use of computer simulation does not, however, can not replace the practical laboratory. However, when experience with aspects of a real experiment is considered important but a practical laboratory only has a limited capacity, then working with a computer simulation program can increase the impact of practical work.
As was said earlier there can be different reasons why the traditional experiment cannot be used in the educational situation, even though the experiment would be desirable because the student's insight could be positively enhanced by doing so. Then computer simulation can be a blessing. We now mention some possible advantages as well as some disadvantages of computer simulation as an educational tool for instruction and training.
Advantages
Some advantages of computer simulation as an educational tool or for training are:
The apparatus necessary to be able to carry out an experiment in reality is too expensive and often this apparatus can only be operated by specialists, if it can be obtained at all. In some vocational training courses e.g. the subject 'robotics' is taught in which attention is paid to the functions and use of a robot. Not every training department however, can afford to buy a robot. But the behaviour of a robot can be imitated by a computer simulation program (see program PLC in figure 1.9). The student or trainee can now exercise as much as necessary. After sufficient exercise the student or trainee may be given the opportunity to handle a real robot in an actual setting. Owing to the practice beforehand precious time and apparatus can be put to optimum use.
The process to be investigated takes place so quickly in reality that it can not be examined through the traditional experiment, e.g. certain chemical processes. Changes in a chemical reaction should be presented at such a pace in educational situations that observation is possible. In reality those changes can hardly be noticed and they are not interesting for calculations, but only for the acquisition of insight (see figure 1.10).
The process to be examined can proceed too slowly in reality, e.g. biological growing processes.
The system to be examined can be too complex for traditional research, e.g. economical systems.
The system to be examined can be on too large a scale, e.g. planetary movements in space.
The system to be examined can be too small, e.g. molecular movements.
The system to be examined can be dangerous to manipulate, e.g. a nuclear reactor, a ship or a human body.
It can be irresponsible from an ethical point of view to do research through traditional experiments as e.g. with certain diseases.
Simulation experiments can be used prior to a course for students or trainees as an introduction to a new subject or certain parts of it (see figure 1.10).
Simulation often goes hand in hand with visualization. The results of changes that a student puts into a model are directly shown on the screen. This generally appeals to students.
Simulation can be very purposive and for certain students very useful, such as students who need some insight before they are able to learn and understand a new concept.
The student can insert those parameter values that he or she thinks will produce a result which is of interest to him. The student can devote his attention to parts that interest him. The student can skip other parts or aspects. This way he or she learns how to experiment systematically.
A student can choose how he or she wants to approach a simulation experiment, how often he or she wants to repeat the experiment and to which degree he or she wants to intervene. In computer simulation there are usually many ways to achieve the goals the student has set himself.
If well-designed, learning how to operate a computer simulation program generally requires little effort. A short introduction by the teacher is often sufficient to enable the student to work with the program.
It can be an advantage that the student perceives that not everything can be used as input. The student realizes that variables and parameters have their limits, and learns what input is reasonable for a particular variable and what input yields relevant information.
Disadvantages
There are not only advantages connected with the use of computer simulation programs in education and training. Limitations are in some cases the result of the wrong or inappropriate use of such programs. Possible limitations of a general and educational kind are:
Simulation concerns the manipulation of a number of variables of a model representing a real system. However, manipulation of a single variable often means that the reality of the system as a whole can be lost. Certain systems or components of a realistic situation are not transparent. Some factors have a lot of influence on the whole, but they have indistinct relations in the whole and can therefore not be represented in a model. These factors, however, cannot be forgotten in the learning process.
A computer simulation program cannot develop the students' emotional and intuitive awareness that the use of simulations is specifically directed at establishing relations between variables in a model. So this intuition has to be developed in a different way.
Computer simulation cannot react to unexpected 'sub-goals' which the student may develop during a learning-process. These sub-goals would be brought up during a teacher-student interaction but they remain unsaid during the individual student use of a simulation.
Computer simulation programs may function well from a technical point of view, but they are difficult to fit into a curriculum.
Often a computer simulation program cannot be adapted to take into different student levels into account within a group or class. A computer simulation program can certainly be made to adapt to different circumstances if the designer bears that in mind; however, for many computer simulation programs this has not happened.
During the experience of interaction with a computer simulation program, the student is frequently asked to solve problems in which creativity is often the decisive factor to success. The fact that this creativity is more present in some pupils than in others is not taken into account by the simulation. Mutual collaboration and discussion among students while using the software could be a solution for this.
Working inductively
Working with a computer simulation program can contain an inductive element that demands an effort from the student. While going through the program the student has to work according to a certain strategy in order to solve the set problems.
This problem is first described and presented as a so-called 'case';. A case can be a part of the program but it may also appear as a text on the screen. It can however also be included in the workbook that is part of the course.
The strategy which has to be followed to solve the problem has an inductive character. After the case is presented the student has to interrupt the computer simulation in order to change the values of the parameters he or she thinks relevant. The results of these changes are then presented on the screen in graphic or table form, in computer voice or through animation. On the basis of the feedback the student can again take action if necessary.
This course of action is repeated until the problem has been solved. Afterwards the teacher can check the worksheets the student has filled in.
Because of the inductive character of the strategy used by the student, computer simulation shows a strong resemblance with all other inductive forms of learning.
Inductive learning is used in researching discovery learning. Foster (1984) writes about the relation between simulation and discovery learning: 'Simulations are excellent discovery learning techniques that often offer insight or 'gestalts' not gained through more traditional didactic methods'.
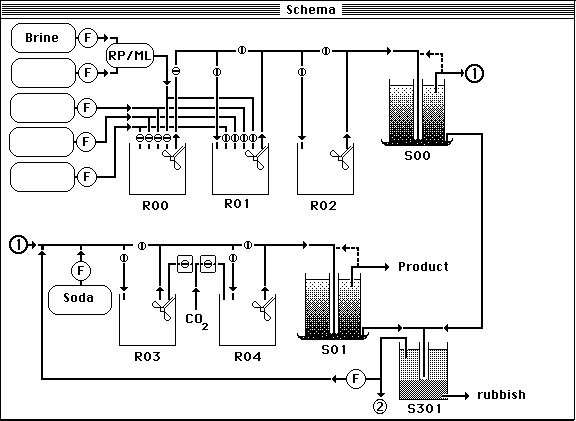
Figure 1.10. The computer simulation program BRINE PURIFICATION / PEKEL built with MacTHESIS (van Schaick Zillesen, 1989) . This program is made for by AKZO, Hengelo, the Netherlands, on Macintosh II computers for the training of plant operators. The model was designed by De Niet of the University of Twente, Enschede (1988) .
1.4 Learning models
A computer simulation program can be used in education in a lot of different ways. We distinguish at least five different using methods in open learning environments on learning with simulation programs of the type of model-driven computer simulations:
discovery learning (without any instruction);
learning by doing an assignment;
coached learning (with instruction materials);
problem guided learning;
learning by doing real (scientific) experiments.
With one computer simulation program all this different ways of using are possable: with or without instruction materials; verbal instruction by the teacher, a set of workingsheets, a workbook or multimedia instruction programs, beside or inside the open learning environment on the screen.
| DEFINITION: A learning model is a qualiative or quantitative (conceptual) model of how students or users find their way in an (simulation) environment.
|
Discovery learning
In discovery learning an unsolved problem is presented or the student is merely exposed to an 'environment' in which he or she can pose a problem to him or herself. For the formulation of the problem and its solution a large amount of self-motivation is required from the student. The intention being for the student to discover the characteristics of a concept, object or system. Bruner (1976) considers this discovery-method to have the following advantages:
By applying the discovery-method the intellectual possibilities of the students increase. They learn to see that there are many possibilities to solve problems and that information has to be translated in a certain way.
The discovery-method heightens the students' intrinsic motivation. The student can take the initiative.
The student learns to handle approaches to problem solving that are useful for the independent solution of new problems.
Knowledge acquired by self-motivation remains better available for reproduction. What you discover for (or make) yourself is easier to remember.
These advantages are also relevant when working with a computer simulation. The output of learning by the method of computer-augmented discovery learning could, however, even be increased if not only in computer simulation, but also within other parts of education more use would be made of the method of discovery learning. However, problems in the sphere of time and material often play a decisive part.
Kolb and Goldman (1973) developed a 'learning model' with regard to the discovery method. He says: 'Learning should be regarded as a cycle consisting of four phases. Concrete immediate experiences form the basis for perception and the resulting reflection. The perception is embodied into a theory from which new assumptions can be deducted. These implications serve as an impetus to collect new experiences.'
Therefore four different skills are required: the skill to acquire concrete experiences, perception, the skill to form abstract ideas and experimenting actively. Perception and experimenting are made easier by simulation.
The contention that computer simulation of systems or situations has an educational advantage in that it stimulates discovery learning is often advanced. But it should be remembered that this happens only when the necessary prerequisite learning of the subsequent concepts has taken place beforehand. This kind of learning leads to the discovery by the student of certain characteristics of a process or phenomenon. With a demonstration in front of the classroom the teacher supplies that which has to be learned.
Much of the information, which is transmitted in a face-to-face, demonstration-by-the-teacher situation, will not reach the student. Mere telling, without confrontation or experiments, can lead to a failing motivation and less enthusiasm in the student. Our education is often amply provided with stimuli and lacking in student response. Time and again we encounter students with a passive listener's attitude. In discovery learning, when conducted in the right way, the student will acquire knowledge that will remain better available for reproduction.
The process of learning in computer simulation can be transformed into a problem solving process. Problem solving has a positive influence on the motivation of the student, demanding activity. During the process adequate insight into the problem area will be acquired. Learning starts with a given problem situation. During the process of learning the student gets insight into means to reach the goals of the problem. This is usually supported by the subsequent discovery of a certain structure, and of a certain reorganization of the problem situation, which leads to the solution.
The total problem has to be split up by the student into a number of smaller problems. During the learning activity the student is activated to find the right solutions for these problems. This way the student needs less encouragement to work. One effect of working with a computer simulation program is that the students' mental flexibility is stimulated and the analytical solution performance can increase.
The problems to be solved with the help of a computer simulation program have to be well-structured and should meet the following conditions:
The set of alternative solutions (hypothesis) is limited and finite.
The solutions are consistently deducted from the model, which in turn corresponds correctly with reality.
The effectiveness and efficiency of the solutions has to be evident.
The solutions (hypotheses) must be controllable by the program.
The problem solving comes about because a representation of the real world in which a problem manifests itself can always be made in the form of hypotheses that can be examined.
The student can do experiments which he or she finds useful, think up a problem and try to solve it. Figure 1.11 shows how the educational learning process can occur while using a computer simulation program this way. Discovery learning without any kind of instruction - paper materials or verbal instructions of a teacher - isn't a successful approach in most of simulation environments.
Learning by doing an assignment
A problem of discovery learning whitout any kind of instruction, is that the student will soon stop with the simulation program if help is not offered in some way, encouraging him to go on. Computer simulation programs do not contain teaching material but provide discovery environments. An important contribution are the exercises or assignments on paper that increase in the level of difficulty. The student can try to work to such an assignment. Before the students run the program they have to put their hypothesis on such a paper to check later on what is writen down and what is happening in the model. The experiment determines immediately if their hypothesis is rejected or not.
A schematic form of the learning process in this book is called a 'learning model'. If there isn't information about the number of times the students do the same loops then we call it a qualitative learning model, otherwise it is a quantitative learning model. An example of a qualitative learning model for learning with pre-programmed cases are given in figure 1.11.
Coached learning by doing
Parallel to the computer simulation program all kinds of coaching is possible and most of the time coaching is very necessary (see also chapter 3: the parallel instruction theory for learning environments). Without a good set of coaching materials, simulation
environments have too much freedom and learning can turn into the wrong way of trail and error. Mostly the coaching in open learning environments involving simulation is done by instruction. Some types of instruction that are possible near simulation are:
verbal instruction by the teacher;
instruction on taperecorder or walkman (mostly parallel and a-synchrone);
a set of workingsheets (parallel; with assignments and/or case discriptions);
a book with instruction materials (parallel);
an intelligent feedback system;
a help system;
a multimedia instruction program
* parallel or in a sandwitch construction:
* synchronous or asynchronous
* tutorial or inquiry;
an intelligent tutoring system (an ITS system).
The method of learning by giving assignments can also be generated by the computer simulation program the moment the computer simulation program 'thinks' that this is possible or necessary in view of previous history and mostly based on Boolean rules. In this book we defined that as intelligent feedback.
| DEFINITION: Intelligent feedback is feedback based on rule-based knowledge system. It can be textual, an audio-fragment, a graphical object, animations or a video-fragment (a 'model-driven message'). |
This method is complicated. But this kind of feedback can be used very well in model-driven simulation environments. Later on we describe that what we call model-driven messages.
| DEFINITION: A model-driven message is feedback which is displayed on the monitor or throughout a speaker and generated by the underlying model or/and a rule-base system. |
The training programs ANAMNESE and MacCOAT for medical students to learn and train history taken with simulated patients, generates multiple-choice questions at unexpected moments depending on how the student goes through the program.
This kind of intelligent feedback in the form of multiple-choice questions isn't a real expert system, but the first step to intelligent tutoring systems (ITS) or intelligent computer simulation programs (ICS programs).
Coaching with the help of an expert system or with computer coaches will not extensively described. Intelligent feedback or model driven messages will be described later.
Problem guided learning
Here a certain way of conducting the model is shown on the screen. Certain variables do something 'abnormal' to the system. The student should analyze the behaviour of the model in order to come to a diagnosis of the presented 'problem'.
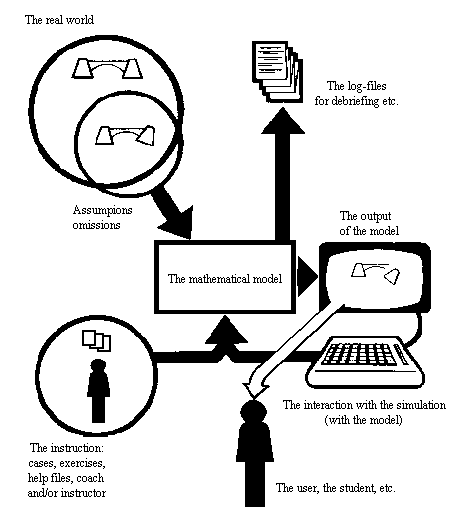
Figure 1.11 Model of the learning process (a 'learning model') in problem-guided-learning, in which there is a pre-programmed case in the computer simulation program accompanied by a text of this case in a workbook.
Figure 1.11 gives a 'model of the learning process' (a 'learning model') in problem guided learning. What happens on the screen is accompanied by paper material on which the student can fill in his first, second and possibly next hypothesis. Generally such cases are supplied with a computer simulation program on loose sheets. Sometimes cases and assignments have been compiled into a workbook.
Learning by doing real experiments
The application of a computer simulation program is in a way that corresponds with practical laboratory work during which something has to be measured. Measuring is done at the values 0.1, 0.2, 0.5 and 1.0 units of a parameter and the corresponding values of a variable are read out and written down. These data then have to be put into a graph either on screen or on paper during such a practical, teaching the student something about the relation between two quantities. This is really a simulation of real scientific research with the reality.
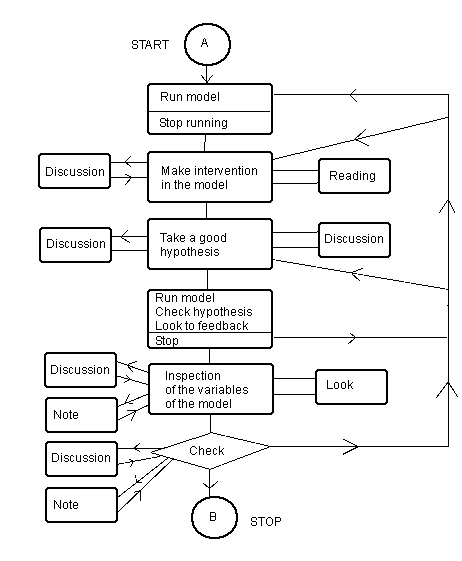
Figure 1.12 Model of interaction in a learning environment with : 'Learning by doing an assignment' and 'Coached learning by doing'.
1.5 Concluding remarks
Finally it can be said that simulation can be used very well for skills in solving intellectual problems in numerous fields, for providing insight into the complexity of reality, and for the training of vocational skills. Simulation does not solve all problems. It works in certain places, especially with certain 'kinds of student' with certain contents. Beside, from an educational point of view, computer simulation models of some human body systems are better than experimenting for educational purposes with simulated systems, such as a rat, as a 'model' of the human body. In that case rats reduce the reality and are not always as good as mathematical models of the intended real system are. Furthermore each computer simulation program can be used in five different ways. Computer simulations are highly adaptive! Coaching materials, like paper materials or CAI materials or intelligent tutoring systems (ITS), is important. Without coaching materials computer simulations are not complete.
( ----> EXTRA TEXT <----- )
Enschede, 1998; updated for interactivity: April 2004












