
MULTIMEDIALE LEERMIDDELEN --- HOOFDSTUK
Een algemeen dynamisch denkmodel voor het bereiken van een doel
(zoals dat voorkomt bij besturen, leren, communiceren en ontwerpen)
Door Rik Min (nog in bewerking; nog in discussie in kleine kring; nog
niet elders gepubliceerd).
Key-words: regelsystemen; feedback, accumulatie, accumulerende systemen, doelen stellen, meten, evalueren, feedback, modellen, quality control.
Samenvatting
Dit artikel gaat over feedback systemen en regeltechniek. Studenten van de faculteit der Toegepaste Onderwijskunde hebben bij een aantal vakken behoefte aan een eenduidig concept aangaande het dynamisch gedrag van besturingssystemen en en andere fenomenen uit hun wetenschappelijke praktijk. Bij TO bestaat al sinds jaar en dag het OKT-model. Dat is een soort procedure, maar feitelijk een denkmodel voor ontwerpen en het bereiken van een doel. Dit artikel beoogt een brug te slaan tussen de wereld van de ontwerpkunde en de regeltechniek. Het moet tevens leiden tot een algemeen toepasbaar dynamisch denkmodel aangaande ontwerpen (een analogon). In dit paper wordt verder betoogd dat dit brede concept-model ook voor andere doeleinden gebruikt kan worden. Dergelijke denkmodellen kunnen worden gebruikt om een beter inzicht te krijgen in het dynamisch gedrag bij het besturen van een bedrijf, het ontwerpen van een product, het zien te bereiken van een communicatief doel en het proberen iets te leren in een wereld met een groot aanbod van bronnen. Alle systemen die een bepaalde waarde (niveau, kwaliteit en dergelijke) meten en vergelijken ten opzichte van een bepaald begin- of gewenst niveau hebben allemaal een belangrijke overeenkomst. De overeenkomst tussen al deze systemen is dat er 'accumulatie' van iets plaats vindt, waarbij de 'sturende' pas tevreden is als er een bepaald eindniveau is gehaald. Men gaat met ontwerpen, besturen, communiceren en leren meestal net zo lang door met een doel bereikt is. Juran is de grondlegger van deze benaderingswijze. Hij noemt dit 'quality control' (Juran, 1954 & 1962).
Het nu volgende artikel doet een poging een algemeen dynamisch denkmodel voor het bereiken van een doel op te zetten; en speciaal een ontwerpdoel. Aangezien deze modellen tot de regeltechniek behoren, gaat dit paper ook in op de mogelijkheden die de regeltechniek biedt en de theoretische kenmerken van gestuurde en/of teruggekoppelde systemen.
Regeltechniek I
De hele maatschappij zit vol met regelsystemen. Overal vind je feedback
systemen en overal heb je te maken met regeltechniek: binnen de economie;
binnen de bestuurskunde; daar waar gecommuniceerd wordt en binnen de biologie, zoals in allerlei ecologische systemen. De regeltechniek is binnen de sociale wetenschappen bijna niet bekend en derhalve vooralsnog niet erg populair.
De regeltechniek komt uit de engineerings-wetenschappen voort. Dit artikel zal laten zien dat de concepten en ideeen daaruit prima kunnen worden gebruikt om het begrip besturing en beheersing theoretisch en inzichterlijk te kunnen benaderen.
Bij de faculteit Toegepaste Onderwijskunde wordt bij het vak 'systeembenaderingen in de onderwijskunde' het 'besturingsparadigma' behandeld. Dit gebeurt in algemene termen en wordt niet zodanig behandeld dat er echt begrip voor deze visie ontstaat en het nut ervan voor iedereen inzichtelijk wordt. Het bestuursparadigma is eigenlijk een te beperkt concept. Mede daarom wordt, hier, in dit artikel, getracht juist de dyamische fenomenen via de schemata van de regeltechniek te benaderen.
Door een betere inzicht in algemene principes en het bepaalde, dynamische gedrag, kan een sociale wetenschapper, een econoom, een onderwijskundige of een ontwerper logischer en inzichtelijker werken.
Een feedback systeem ziet er in zijn algemeenheid uit zoals in figuur 1 is aangegeven. Er is een 'primair proces' (het besturende systeem) (B.S.), een 'feedback loop', een 'besturingsapparaat' (B.O.) en een exclusief aangegeven systeem om het verschil tussen de gemeten waaarde en de ingestelde waarde te vergelijken. We noemen dat hier voorlopig een 'comperator'. Daar worden twee vergelijkbare grootheden met elkaar vergeleken. Het verschil noemen wij de 'error' (of afwijking). Die 'error' moet zo klein mogelijk worden; het liefst nul. In een dergelijk systeem kun je iets bereiken door je een doel te stellen en te kijken of het doel bereikt is of wordt. De tijd welke nodig is dat doel te bereiken is belangrijk; die zegt iets over de eigenschappen en de mogelijkheden van het betreffende systeem.
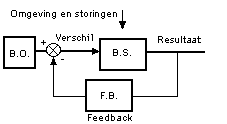
Figuur 1. De afzonderlijke onderdelen van een systeem: het 'bestuurd systeem' (B.S.), de terugkoppellus en het 'besturend orgaan' (B.O.) (o.a. Kramer en De Smit, 1991). Duidelijk te zien is een feedback loop. Een evaluatiemoment is essentieel om de 'kwaliteit' van het 'product' te kunnen bewaken. Zonder feedback-loop zou men nooit het product (qua 'kwaliteit') in overeenstemming kunnen brengen met een gewenste waarde. Het resultaat van de inspanning wordt gemeten. Dit is dan ook wat regeltechnici een metend en teruggekoppeld systeem noemen.
Het primaire proces kan een fabriek, een apparaat, een auto, een schip, een
vliegtuig, een dienstverlenend orgaan of een groep mensen zijn die iets doen. Stel dat dit primaire proces
niet bestuurd wordt, dan is er dus ook geen feedback nodig om het
'bestuurend apparaat' van informatie te voorzien. We spreken dan van een
feedforward systeem. Elders wordt beschreven wat de voor- en nadelen van
een dergelijk systemen - zonder over-all feedback-loop - zijn (Min, 1999).
Een feedback systeem kan zelfsturend zijn, maar ook bestuurd worden. We noemen het fenomeen van automatische controle, d.w.z. zelfsturing, dus mechanismes die automatisch, zonder dat er iets aan te pas hoeft te komen, hun werk doen: homeostase. Bij systemen die we hier beschrijven is zelfsturing op zich niet direct aan de orde. Daar zit het doel niet 'ingebakken', maar wordt het doel meestal door 'iets' of iemand anders gesteld. We geven van beide soorten systemen enkele voorbeelden.
Voorbeelden van zelfsturende systemen (zelfregulatie):
Voorbeelden van de eerste kunnen allerlei gestuurde, dynamische processen in het menselijk lichaam zijn. De lichaamstemperatuur wordt bijvoorbeeld, op één of andere manier, door een regelmechanisme constant gehouden.
Een ander voorbeeld is de markt. Vraag en aanbod van een of ander product wordt in de praktijk in het algemeen gelijk gehouden. Als de prijs zakt daalt het aanbod; als het aanbod daalt stijgt de prijs (weer). Een bepaalde schommeling rondom een nominale waarde is hierbij normaal en zelfs inherent aan systemen met zelfsturing.
Voorbeelden van stuurbare systemen:
Voorbeelden van de tweede mogelijkheid, stuurbare of gestuurde systemen, zijn als we bijvoorbeeld besluiten hard te gaan lopen, i.p.v. wandelen. We kunnen met lopen dus verschillende doelen hebben. We geven ons lichaam bijvoorbeeld de opdracht hard te gaan lopen. We stellen ons dus een doel, namelijk onze benen - op een bepaalde gewenste snelheid - te laten hollen (goal B). We kunnen ook besluiten gewoon te gaan wandelen. Dat is een heel ander doel (goal A). Pijn kan dan bijvoorbeeld een feedback mechanisme zijn dat ons doet besluiten iets minder hard te lopen. Ook het horloge kan als een feedback mechanisme fungeren. Als we bijvoorbeeld de trein dreigen mis te lopen - en we zien dat op ons horloge - besluiten we sneller te gaan lopen.
Een tweede voorbeeld is het besturen van een schip of een auto. We draaien net zo lang aan het stuur tot de bocht die we willen nemen genomen is. Het oog van de bestuurder is het meetinstrument dat de feedback geeft. Bij een schip moeten we ons echter realiseren dat de 'tijdconstante' hierbij veel groter is dan bij een auto.
Een derde voorbeeld is het ontwerpen en het maken van een product. We stellen ons een doel, een kwaliteit, en we proberen dat doel, die kwaliteit, te halen. We doen dat zo goed mogelijk. Daarna wijst een eenvoudige test of een formatieve evaluatie al dan niet uit of we ons doel hebben bereikt.
Een vierde voorbeeld is het besturen van een bedrijf of een dienstverlenend orgaan. Als de winst of de productie achterblijft, besluiten we harder te gaan werken. De manager van het bedrijf of de chef van een afdeling bepalen zulke dingen.
Een vijfde voorbeeld is een student die heel bewust een traject ingaat om iets te leren en examen doet (Min, Vos, Kommers, Van Dijkum, 1998). Merkt hij dat hij de stof niet beheerst dan doet hij er een schepje boven op. Denkt hij - om een of andere reden - dat hij de stof geheel beheerst, dan studeert hij niet verder en doet zo tentamen. De uitslag van het tentamen is zijn feedback. Dan blijkt wel of de gemeten waarde overeenstemt met de gewenste waarde.
In al deze voorbeelden stelt iemand zich een 'doel' of neemt een besluit over iets. Meestal is dat een te bereiken doel. Het besturend apparaat zegt dat, vanaf een zeker moment, niet meer naar doel A gestreefd dient te worden, bijvoorbeeld niks doen, maar naar doel B. Dit fenomeen van besluitvorming en doelen stellen noemen we (hier) het 'set point' voor 'het systeem'; feitelijk het set point voor het primaire proces: de fabriek gaat aan het werk; de hardloper gaat hardlopen; de auto gaat rijden; het dienstverlenend apparaat gaat iets doen; de ontwerper gaat zijn eerste prototype maken. Om processen als dit te kunnen beheersen heb je dus altijd 'goals' en minstens een feedback mechnanisme nodig, want je moet weten of je je doel hebt bereikt.
Rond 1994 was er in Enschede een conferentie op de campus van de
Universiteit Twente of ontwerpen een wetenschap is. In 1997 volgde er een conferentie over "Design Methodologies and the Social and Behavioral Science Professions". Dat laatste gaf de aanzet voor het schrijven van dit artikel. Het was een conferentie over de fundamenten van ontwerpen binnen de sociale wetenschappen en georganiseerd door de projectleiders: A. Rip, Tj. Plomp en J. Moonen. Het project waar deze conferentie onderdeel van was startte in 1995 en is door de Universiteit Twente gefinancierd. Het diende een brug te slaan tussen ontwerpers uit een groot aantal disciplines binnen de sociale wetenschappen. Er werden enkele visies op ontwerp-modellen gegenereerd en enkele knelpunten gesignaleerd. Moonen kwam ten slotte in 1998 met een een zeer complex model over ontwerpen. Het model oogt vrij onpraktisch. Het geeft niet echt inzicht in de dynamiek van ontwerpen; wel in de opeenvolgende fases van een ontwerp-proces (Moonen, 1998). Dat is feitelijk nog steeds iets te kookboek-achtig.
Op 28 maart 1997 verscheen in NRC/Handelsblad een artikel "Cursisten in de mist" van J. Kuijpers. Dit was de tweede aanleiding voor het schrijven van dit artikel. In gesprek met bedrijfsopleiders, die kampten met dezelfde soort problemen als op deze conferentie werden beschreven, werden door de auteur vragen opgeworpen zoals: "hoe gaat men om met goals en feedback?" De teneur van deze analyse was dat zonder doelen en zonder evaluatiemoment een heleboel cursussen als het ware een schot in de ruimte zijn. Men kan zich afvragen of cursisten wel weten dat dat slechte cursussen kunnen zijn.
Bedrijfsopleiders weten als geen ander dat er bij cursussen waar cursisten
geen doel hebben en de opleiding niet geëvalueerd wordt er binnen de kortste tijd discrepantie ontstaat tussen het gewenste en het bereikte doel.
In dit artikel zal het dan ook gaan over 'meten', het stellen van doelen, vormen van feedback en het vergelijken van twee toestanden. Het zal een zoektocht zijn naar de overeenkomsten in het ontwerpen van bijvoorbeeld een leermiddel, een cursus, een curriculum als product. Maar ook een product als een campagne-plan of een organisatie-advies kan als ontwerp-product onder de loupe worden gelegd. Dit artikel wil een bijdrage leveren aan het goed kunnen doorzien van het primaire proces van het stellen van doelen en dat men beseft dat men net zo lang door moet gaan tot het einddoel ook werkelijk bereikt is. Anders krijgt men nooit een bepaalde kwaliteit en kan men niet vergelijken.
Alle bovengenoemde voorbeelden geven aan hoe belangrijk men het vind om binnen de onderwijskunde uit te vinden hoe ontwerpen - dynamisch gezien - in zijn werk gaat. In dit paper wordt beoogt dat de regeltechniek een bijdrage kan hebben in het vinden van goede modellen voor ontwerpen. Dit artikel gaat zelfs verder; er wordt gesteld dat de regeltechniek die denkmodellen niet alleen kan opleveren, maar ook denkmodellen levert die meer kunnen dan alleen iets te betekenen voor ontwerpen.
Regeltechniek II
Regelsystemen hebben allen hun eigen kenmerken, zoals een bepaalde snelheid van reageren en/of een 'dode tijd'. De snelheid van reageren wordt een 'tijdconstante' genoemd. De tijd die nodig is om - in de voortgaande weg - een effect te sorteren wordt de dode tijd genoemd. Een dode tijd van een systeem, in combinatie met een (verkeerde) tijdconstante of een (verkeerd) doel, kan een regelsysteem of een geregeld systeem instabiel maken (Min, 1998). Daar gaat dit artikel verder niet op in.
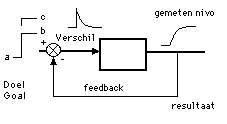
Figuur 2. Dit is een afbeelding van
een algemeen teruggekoppeld systeem ook wel een feedback systeem genoemd.
Dit systeem is regeltechnisch van belang. We kunnen nu zeggen hoeveel het
verschil is tussen de gewenste en de gemeten waarde. Het
verschil in een feedback systeem gaat altijd naar nul. De curve die daarbij
hoort komt overal in het dagelijks leven voor: in de sociale wetenschappen, psychologie, natuurkunde, etc.
Als er geen goed feedback systeem is of als er geen goede signalen van het
primaire proces naar een beslisser worden getransporteerd kan een beslisser
onmogelijk goed besturen. Het primaire proces kan immers doen wat zij wil en daarmee haast onmogelijk een goed 'product' leveren. Wij noemen een slecht 'product' hier 'slechte kwaliteit'. Het is Jordan geweest die in 1946 deze vorm van besturen, beheersen en regelen daarom 'quality control' heeft genoemd (Jordan, 1962).

Figuur 3. Hier ziet u een gewone klassieke regelkring, maar wel anders
opgezet (getekend) dan in figuur 1.
In veel wetenschapsgebieden heeft het denken over 'quality' nog niet de aandacht
gekregen die het verdient. Dit komt wellicht omdat men bij de begrippen
'product', 'quality' en niet op de laatste plaats bij het woord
'regeltechniek' allerlei negatieve assosiaties krijgt. De wereld van de
dienstverlening heeft dertig jaar nodig gehad om het puur zakelijke
(en hier dus technische) woord 'product' van zijn fysieke lading te
ontdoen.
Zonder een goed plan kan een ontwerper niet ontwerpen. Zonder goede feedback
kan een ontwerper niet beoordelen of zijn product 'af' is. Immers langs welke meetlat leg je iets en wat is de maatstaf? Zonder doel kan een automobilist niet rijden (goal). Zonder zijn ogen te gebruiken kan een automobilist niet naar het gewenste punt rijden (feedback). Hoe vergelijkt men het actuele, bereikte en gemeten resultaat (result) met het gewenste resultaat (goal)?
Daar is een vergelijker (een 'comparator') voor nodig. Dat element is in figuur 2 duidelijk te onderscheiden.

Figuur 4. Dit is het Quality Control systeem van Juran. Duidelijk is te zien een
sensor, een effector en een (lineair) process. Verder is het 'set-point'-gedeelte en de 'vergelijker' (c.q. 'comparator') te zien. (First published by Juran, Planning and control; 1954)
Het OKT-model kent een feedback-lus waarbij de evaluatie (het 'meten') het belangrijkste onderdeel van is. En dat is niet toevallig. Als je immers een evaluatie inbouwt - hoe klein en eenvoudig dan ook - vrijwaar je jezelf tegen risico's. Bij een feedback-loos systeem zoals een feedforward-systeem zijn er namelijk wel bijna altijd problemen. De kwaliteit van het resultaat is niet controleerbaar. Als de kwaliteit gemeten wordt en er is feedback, dan regelt het systeem zodanig bij net zo lang totdat het resultaat en/of het product in orde is. Zie de feedback-loop bij het OKT-model in figuur 8. Zie ook de literatuur over de theorie van Quality Control van o.a. Juran, 1962 (eerste druk) en Bush & Mosteller, 1955. Feedforward systemen, dus systemen zonder feedback-mechanisme, zijn in de praktijk volkomen onhanteerbaar als je precies een vooraf besloten doel wil behalen; laat staan als er tussentijds allerlei storingen optreden in het proces of tegenvallers om de hoek komen kijken.
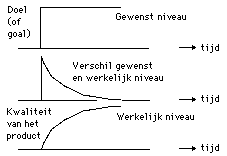
Figuur 5. De drie belangrijkste curves als functie van de tijd. De bovenste curve: het 'doel' dat men zich in het begin op een zeker tijdstip stelt. De onderste curve: het niveau van de 'kwaliteit van een product' groeit - om een of andere reden - in de loop van de tijd. Het product gaat uiteindelijk steeds meer aan de verwachtingen voldoen. Het bereiken van die kwaliteit kost tijd. De tijd in deze figuur kan gemeten worden in minuten, uren, dagen of jaren. De groeisnelheid hangt verder af van de 'tijdconstante(n)' van het systeem. De middelste curve: het verschil tussen de gewenste waarde en de werkelijke - gemeten - waarde; en zijn zeer karakteristieke verloop in de tijd.
Dit artikel handelt feitelijk over dat wat Juran in 1962 'Quality Control' heeft genoemd (Juran, 1962). Dit syteem-denken van Juran is - naar mijn overtuiging - een prachtig voorbeeld van regeltechniek. In zijn feedback systeem (zie bijlage) kan de kwaliteit van een product of een proces altijd worden bereikt. Men dient een goede planning te maken. Men moet een plan hebben en/of een norm 'setten'. Dat wordt het 'set point' of de gewenste waarde - hier de gewenste kwaliteit - genoemd. Door een (goede) controle, d.w.z. een controle aangaande het verschil tussen de gewenste waarde (set point) en gemeten waarde (result), is het resultaat op termijn - wat er ook gebeurd - altijd gelijk aan de gewenste waarde.
Juran gaat uit van drie belangrijke grootheden voor quality controle: 1. planning, 2. controle en 3. (voortdurende) verbetering. In alle fasen van een productieproces moet controle zijn. Dan krijg je een stabiele kwaliteit en kun je veranderingen in kwaliteit uitsluiten.
Beslissingen nemen
Elk feedback systeem kent een input en een output. De input is een beslissing om iets te gaan doen; het doel. Men beslist van niveau A naar niveau B te gaan. Een directie van een bedrijf kan besluiten, om i.p.v. 100 auto's per dag, 200 auto's per dag te gaan produceren of een student kan besluiten, om i.p.v. van twee colleges, drie colleges gaan volgen of iemand kan besluiten om 10 km per uur, i.p.v. 5 km per uur, te gaan lopen.
Figuur 2 laat enkele van die situaties zien. Het kenmerk van de hier besproken regelsystemen is de plotselinge omslag van waarde a naar een andere waarde: b of c. Het is meestal een accute beslissing of een doel-wijziging welke van de een op het andere moment gesteld wordt. Langzame doelveranderingen zijn gecompliceerder, maar feitelijk zijn langzame doelveranderingen altijd opgebouwd uit kleine, stapsgewijze doelveranderingen.
Output hangt primair af van de karakteristieke eigenschappen in de 'voortgaande weg' of - zo men wil - het 'voorwaartse systeem of het 'bestuurd systeem' (B.S.). Een systeem zonder feedback-loop is dan een feedforward-systeem geworden. Het gedrag van het 'bestuurd systeem' (B.S.) is bepalend voor het gedrag van het gehele systeem (mèt feedback). We noemen dat gedrag van het 'bestuurd systeem' (hier) het 'intrinsieke gedrag' van een systeem. In het boek van Kramer en de Smit (1991) worden de 'versterking' K en de 'tijdsvertraging' tau als de meest belangrijke eigenschappen van het bestuurd systeem gevonden. Een systeem mèt feedback-loop gedraagt zich volstrekt anders, maar toch kan de regeltechniek voorspellen hoe en wat het gedrag is t.o.v. de grootheden K en tau. Het gedrag van een feedback-systeem in de tijd, wordt echter op een bepaalde manier volledig door de grootheden van het voorwaartse systeem bepaald. Bijvoorbeeld de tijdsconstante van het teruggekoppelde systeem ligt hiermee volledig vast.
De output van een feedback systeem kent ten opzichte van een stapvormige input vijf karakteristieke soorten responsies. Kramer en de Smit beschrijven dat in hun boek op pagina 74. Het zijn:
1. snel (of langzaam) oplopend vanaf de beginwaarde a en daarna langzaam uitkomend op de eindwaarde b;
2. snel (of langzaam) oplopend naar een waarde groter dan b, maar wel weer terug en uiteindelijk na een of twee overshuut-, resp. ondershuut-reacties toch uitkomend op de eindwaarde b;
3. heel langzaam oplopend vanaf de beginwaarde a en daarna sneller om toch weer langzaam uit te komen op de eindwaarde b;
4. snel (of langzaam) oplopend naar een maximale waarde, maar uiteindelijk weer terugkomend op de beginwaarde a;
5. een opslingerend fenomeen met een onduidelijke, maar (zeer) hoge eindwaarde die totaal niet meer de waarde a bedraagd.
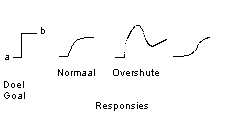
Figuur 6. Enkele fundamentele verschillende soorten van responsies.
Figuur 6 geeft de drie belangrijkste responsies aan: een zogenoemde 'eerste orde' regelsysteem; een zogenoemd 'tweede orde' regelsysteem en een afwijkend regelsysteem (met vertraging). Een specialist kan aan het gedrag van de output bijna alles wat regeltechnisch belangrijk is, aflezen. De output geeft bijna alles van zowel het B.S.-gedeelte als van het B.O.-gedeelte prijs. Een specialist kan hiermee de zogenoemde 'regelkarakteristiek' bepalen. Het karakter van de 'regelkarakteristiek' is op zijn beurt bepalend voor de manier waarop men met een dergelijk systeem om kan gaan en hoe men een dergelijk systeem moet of kan besturen en stabiel kan houden. Stabiliteit is in de regeltechniek bijna alles bepalend. De karakterisieken van het geheel van een feedback systeem liggen vast als men de karakteristieken van de 'bestuurd systeem' (B.S.) kent. Men kan dan 'regeltechnisch' (dus wetenschappelijk) bepalen wanneer een teruggekoppeld systeem uit zich zelf instabiel wordt of wannneer - en onder welke voorwaarden - een bepaalde 'beslissing' - bijvoorbeeld wanneer b te groot t.o.v. a en t.o.v. andere eigenschappen van het systeem - instabiel kan worden. Als K heel groot is en als tau kritische waarden bereikt, wordt het systeem, dat eerst stabiel was, juist instabiel.
In de figuren 3 en 5 is het karakteristieke verloop te zien van (eerste orde) regelsystemen. Regelsystemen zonder overshuut kunnen we als eerste orde regelsystemen definieren; systemen met overshuut zijn meestal regelssystemen van 2e of hogere orde. (Zie .....)

Figuur 7. In deze figuur is te zien hoe bestuurders een inspanning doen (en gedaan hebben) toen zij (destijds) bemerkten dat de gemeten waarde van hun ideaal stagneerde. Steeds als de waarde van deze variabele stagneerde (en het model in een steady state kwam) gooide men er een schepje bovenop. Dit patroon is zeer karakteristiek en komt overal in de regeltechniek bij systemen met feedback mechanismes voor. Volgens: McAfee & McMillian, Analyzing the airwaves Auction, J. of Economic Perspectives 10:1 (1996) pp. 159-175.
In figuur .... is het ideale theoretische verloop te zien van (eerste orde) regelsystemen en in figuur ... het verloop van een relatief willekeurig ander (eerste orde) besturingssysteem. Het meest kenmerkende van eerste orde regelsystemen is het oplopende (cummulerende of accumulerende) 'resultaat' en dientengevolge het in het begin het grootst mogelijke verschil tussen het 'doel' en het 'resultaat'. Dat verschil wordt pas na verloop van tijd kleiner en kleiner en tenslotte bijna nul. In figuur ... is goed te zien dat 'beslissers', op de momenten dat het 'gemeten resultaat' stokte, en de 'output-curve' dus vlak ging lopen, steeds pogingen ondernamen (en inspanningen gingen leveren) probeerden het resultaat op te krikken. Tussen het start-moment 0 en 12 gaf men afnemend 'injecties'; tussen het moment 12 en 64 gaf men afnemende injecties en tussen het moment 52 en 112 ook. Blijkbaar gaat de output niet uit zich zelf omhaag en moet men dit systeem blijven voeden. Of men dient genoegen te nemen met het bereikte niveau. Zonder inspanning (van buitenaf) gaat de 'output' van dit systeem (blijkbaar) niet (verder) omhoog. Dit voorbeeld uit de 'Journal of Economic Perspectives' is gekozen omdat het exemplarisch is voor een eerste orde regelsysteem waarbij 'accumulatie' te zien is. Deze vorm van regelen en fenomenen waarbij accumulatie een rol speelt, komen veel voor.
Accumulerende systemen
Feedback systemen zijn over het algemeen niet-lineaire regelsystemen. Toch zijn feedback-systemen voor een klein deel altijd wel lineair; als het bijvoorbeeld om twee of drie (kleine) veranderingen aan de input-kant gaat. De output-kant vertoont wel degelijk, na een bepaalde, zeer karakteristieke tijd vaak een lineair gedrag aan de output-kant. Bij het draaien aan een stuurwiel is het meestal wel zo, dat door het twee of drie keer linksomdraaien van een stuurwiel het voer- of vaartuig - meer dan bij een keer draaien - naar links koerst. Dat duidt op het partieel lineair zijn van veel systemen. Bij het hier beschreven model van leren of van ontwerpen is het duidelijk dat een twee maal zo grote inspanning niet per definitie leidt tot een twee maal beter resultaat. Integendeel. In de curves van het resultaat versus een 'inspanning' per tijdselement is te zien dat als het niveau bijna bereikt is er vaak een bijzonder zware inspanning nodig is om nog een beetje hoger niveau te halen. Dat is in principe allemaal uit figuur ... af te leiden. Min beschreef dit niet-lineaire fenomeen al in 1986 in zijn eerste, Nederlandstalige boek (Min, 1986). In 20 procent van de projecttijd wordt meestal 80 procent van het doel bereikt, maar daarna kost het 80 procent van de projecttijd om uiteindelijk echt, dus 100 procent, een doel te bereiken.
Het model van leren dat we hebben opgesteld kent ook dit accumuleer-gedrag. Er zijn vele modellen die dit accumuleren vertonen: o.a. het model voor ontwerpen, maar ook modellen voor het besturen van organisaties.
Ontwerpen
Ontwerpen is een bezigheid waarbij men een bepaald plan heeft en
waarbij men een proces in gaat en uiteindelijk het product evalueert. Een
evaluatie is het op é'éeen of andere manier meten van de gewenste kwaliteit van het product. De afweging of iets aan de verwachting heeft voldaan is
een tweede en wordt meestal aan anderen over gelaten. Ontwerpen lijkt
welliswaar niet zo dynamisch als regelen, maar toch is het ontwerpproces
een geregeld systeem. Er is een 'doel'. Er is een 'proces'. Er is een
'evaluatie' en een 'beslissingsproces'. Uiteindelijk is er een groen of
een rood licht; go or not go.
Als we ontwerpen binnen de sociale wetenschappen in grote lijnen
opvatten als een proces zoals door Plomp et. al. (1992) is beschreven, dan
valt op dat ondanks de grote hoeveelheid kritiek die dat model door de
jaren heen heeft gekregen, het nog steeds door iedereen als een goed
vertrekpunt wordt gezien. Dit geldt zeker voor onervaren ontwerpers en het
is dus ideaal voor studenten tijdens hun studie. Er is feitelijk geen
eenvoudiger alternatief. Alleen de 'rapid prototyping'-methode wijkt af. Daar wordt tijdens het ontwerpen en het zien realiseren van het product het doel steeds bijgesteld. Een beetje te vergelijken met wat in figuur ... wordt geprobeerd uit te leggen: jezelf steeds een ander, hoger doel stellen en dat doel proberen te halen. Maar als er wordt doorgedacht, is het OKT-model van Plomp zelfs in de situatie van 'rapid prototyping' uitstekend bruikbaar.


Figuur 8. Het OKT-model van Plomp e.a. (boven). Duidelijk is de feedback loop te zien. Het evaluatiemoment is essentieel om de 'kwaliteit' van het 'product' te kunnen bewaken. Dat is feitelijk de comparator. Zonder feedback-loop zou men het product (qua 'kwaliteit') nooit in overeenstemming kunnen brengen met een gewenste waarde. Als we het OKT-model een kwart slag draaien zien we feitelijk een gewoon regelsysteem met al de eigenschappen zoals die in de tekst worden beschreven.
Als je het OKT model (links) een kwartslag draait is het een feedback
systeem met een 'meetmoment' (de evaluatie) en een terugkoppellus die zo
vaak wordt doorlopen tot dat de gemeten waarde gelijk is aan de gewenste
waarde (rechts). Een ontwerper wil (ook) een verschil van nul tussen de
gewenste waarde en de gemeten waarde. De ontwerper gaat net zolang door
met het bijschaven van zijn product of oplossing tot het gewenste
resultaat ('goal') is bereikt. De ontwerper stopt dan.
Dit is in
figuur ... goed te zien.
Het 'primair proces' (B.S.) bij het OKT-model is het zien te realiseren van het product. Het 'besturingsapparaat' (B.O.) is het doel dat de ontwerper zich stelt. Dat doel komt meestal voort uit de voorstudie. Het verschil tussen de 'gemeten waarde' en het 'doel' wordt met elkaar tijdens de evaluatie vergeleken. Als het verschil, de 'error' nul is stopt de ontwerper met het bijschaven en is het product klaar.
Binnen de onderwijskunde wordt er traditioneel weinig onderzoek gedaan
naar het opstellen van deterministische modellen die verschijnselen kunnen
vastleggen en nabootsen zoals die zich voordoen bij ontwerpen. Er wordt
wel veel onderzoek gedaan naar de methodologie van ontwerpen, maar meestal zijn dat kookboek-achtige producten en ontwerpregels. Maar hier, in dit artikel, willen we dat niet als onderwerp van discussie nemen.
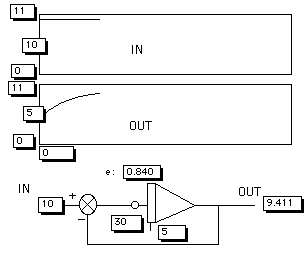
Figuur 9. Het hart van het voorgestelde regelsysteem draait op een PC. De overdrachtsfunctie (B.S.) in dit model is zo eenvoudig mogelijk gehouden. Het B.S. gaat net zo lang door met zijn (opgedragen) actie tot OUT gelijk is aan IN. D.w.z. totdat e = 0. Dit werkende prototype is gerealiseerd door Min en heeft voorlopig de naam 'FEEDBACK versie 1.0x' gekregen (Min, 1999). In deze screendump is goed te zien dat het doel van de 'bestuurder' was om het systeem van nivo '5' op nivo '10' te brengen en dat het verschil tussen de gemeten waarde (9.411) en de gewenste waarde (10) bijna nul is (0.840). Derhalve is het doel (10) bijna bereikt. Het model geeft dat allemaal keurig netjes grafisch in de tijd op het scherm aan.
Resultaten
Om een en ander ook nog inzichtelijk te maken heeft Min een aantal modellen gebouwd en in simulatieprogramma's uitgetest. In figuren 6, 7a en 7b zijn de programma's 'LEREN', 'DIFFUSIE' en 'BEDRIJF' te zien. Al deze simulaties zijn gebaseerd op het hierboven beschreven eerste orde regelsysteem. Het zijn pre-prototypes. De samenhang tussen deze drie prototypes is dat al deze programma's zijn gebaseerd op het hier beschreven regelmechanisme van 'Quality Control' van Juran. Het model van leren is eerder beschreven (Min, Vos, Kommers en v. Dijkum, 199...). Het programma DIFFUSIE is het zogenoemde broadcast model van ....... en beschreven door Vos (Vos & Min, 199...). Het laatste programma, het pre-prototype BEDRIJF, is recentelijk door Min ontwikkeld aan aanschouwelijk aan te tonen dat dit soort modellen goede 'denkmodellen' kunnen zijn voor hoe een land of bedrijf wordt geregeerd of bestuurd.
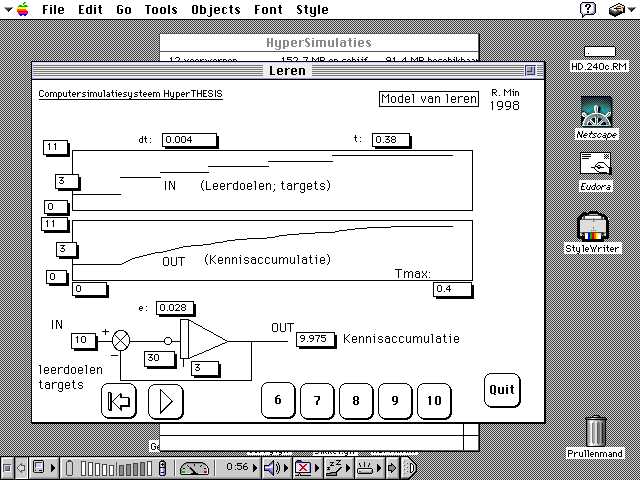
Figuur 10. Een model voor kennisvergaring. Het programma LEREN, versie 2. U ziet in dit simulatieprogramma, waar het model voor leren in verwerkt is, dat er een aantal doelen zijn die leerlingen zich zelf kunnen stellen. Men komt dan uit op een bepaald kennisniveau. Men begint op niveau 3 en men kiest doel (of niveau) 6, 7, 8, 9 of 10. In dit voorbeeld heeft men op tijdstip t=0 als doel 5 gekozen en op tijdstip t=0.1 als doel 9 gekozen. (Het beginniveau van de leerling was 3.) U ziet dat de leerling de niveaus na een zekere tijd bereikt. (Min, Kommers, Vos en Van Dijkum, 1998)
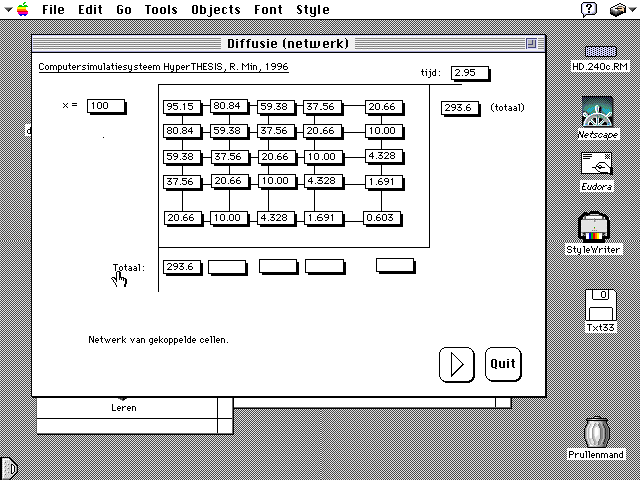
Figuur 11. Hier is te zien hoe een boodschap zich 'vanzelf' - door diffusie - over een populatie verspreid. Het programma DIFFUSIE (Min, 1998) is gebaseerd op het braodcast model van ....
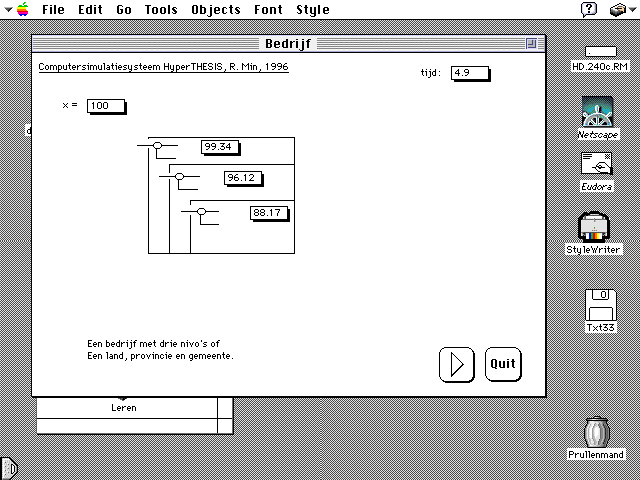
Figuur 12. Hier is te zien hoe men op macro-niveau een besluit kan nemen; op meso niveau en op micro-niveau. Dit is het programma BEDRIJF (Min, 1998). Met dit programma is te zien hoe een beslissing wedijvert met een beslissing welke op een ander niveau is genomen.
Met het programma LEREN kun je zien hoe het doel welke een leerling zich zelf stelt, kan worden bereikt. Men komt dan uiteindelijk uit op een gewenst kennisniveau. Men begint op een bepaald niveau en kiest een verderliggend doel. In het voorbeeld ziet u dat de leerling de niveaus die hij nastreefde, na een zekere tijd ook daadwerkelijk bereikt. (Min, Kommers, Vos en Van Dijkum, 1998)
Met het programma DIFFUSIE (Min, 1998) kun je zien hoe een boodschap zich door het mechanisme van diffusie over een populatie verspreid. Het programma is gebaseerd op het braodcast model van ....
Met het programma BEDRIJF (Min, 1998) is te zien hoe men op drie verschillende niveaus een besluit kan nemen: op macro-niveau; op meso niveau en op micro-niveau. Het programma heeft visuele output waaraan je kunt zien hoe en waar de uitwerking plaas vindt. Met dit programma is dynamisch en visueel te zien hoe een beslissing op een bepaald niveau wedijvert met een beslissing op een ander niveau.
Discussie
Doordat dit soort modellen gebaseerd zijn op dynamische modellen en de betreffende programma's ook nog allerlei visuele output hebben, is het onderliggende fenomeen goed inzichtelijk te maken. De gebruiker - of het nu een leek is of een professional - krijgt een goed en kwalitatief betrouwbaar inzicht in een fenomeen. We werken nog aan beter ontworpen en vormgegeven progrmma's. Maar duidelijk is in ieder geval dat zonder een dergelijk simulatieprogramma dat onderwijskundige doel niet zo gemakkelijk zou zijn te bereiken.
We hopen de overeenkomsten tussen al deze benaderingswijzen, modellen en programma's later
nog eens beter aan te kunnen tonen. Vooralsnog willen we onze opvattingen en bevindingen publiceren. Als we het leggen naast het ideeën dat schema's (zoals dat van Plomp) eigenlijk niets anders zijn dan feedback systemen en zich gedragen conform de theorieen uit de regeltechniek - en dat kunnen we aantonen - dan moet
onze benadering serieus worden genomen.

Figuur 13. Hier is een functioneel diagram afgebeeld, waarin de belangrijkste opdrachten of functies van Quality Control zijn neergezet. het inspecteren, het controleren en de kwaliteitsgarantie (aangaande het eindproduct). (First published by Juran, Planning and control; 1954)
Een onderwijskundige oplossing voor een onderwijskundig vraagstuk, een onderwijskundig product, kent - als het goed is - altijd ergens een 'meetmoment' (de evaluatie) en een terugkoppellus; een lus die zo vaak wordt doorlopen tot dat de gemeten waarde gelijk is aan de gewenste waarde (b). Een ontwerper streeft daarna.
We hebben geprobeerd aan te tonen dat de belangrijkste functies uit het model van Quality Control van Juran (zoals het inspecteren, het controleren en de kwaliteitsgarantie aangaande het eindproduct) een goed aanknopingspunt was en is voor een brede discussie over modelvorming, aangaande deze onderwerpen uit de sociale wetenschappen.
Figuur 8 laat zien dat ontwerpen in principe cyclisch verloopt en dat een einddoel en feedback daarbij essentiele dingen zijn. Bovengenoemde model voor ontwerpen geeft daarom nog beter inzicht in wat ontwerpen eigenlijk is, en zegt tegelijkertijd iets over de dynamica van de ontwerpcyclus. Het model dat we hier voorstellen is derhalve een analogon voor ontwerpen.
De schrijvers hopen met dit artikel en met de hier beschreven prototypen een bijdrage geleverd te hebben aan de spraakverwarring bij dit soort fenomenen.
Conclusies
Aan de modellen moet nog veel geschaafd worden. Er zal nog veel commentaar komen. Dat zullen we verwerken tot betere modellen of concepten.
Het model staat nu nog in de kinderschoenen, maar het concept is hiermee voor de discussie vastgelegd. Veel details moeten nog verder worden uitgewerkt en worden onderbouwd. O.a. zullen de tijdsconstantes verder uitgezocht moeten worden. De modellen moeten - zeker op dit punt - getoetst worden aan de tijdschaal bij/in werkelijke processen. Verder onderzoek moet dan uitwijzen of dit model een plausibele (kwantitatieve) verklaring kan bieden voor dit soort accumulerende fenomenen zoals 'leren', 'communiceren', 'ontwerpen' en 'besturen'. Fenomenen die juist in samenhang en dynamisch - in de tijd - zo belangrijk zijn om goed begrepen te worden.
Referenties
Juran (1962)
Quality Control. Uitg.: MIT, Cambridge, USA. (vernieuwde druk)
Juran (1954)
Quality Control. Uitg.: MIT, Cambridge, USA. (1e druk)
Vos, H. en Min, R, (1997)
Systeembenaderingen in de onderwijskunde, Studiehandleiding,
TO/Universiteit Twente, Enschede, (cursusjaar 97/98)
Kramer, N.J.T.A., en J. de Smit; Systeemdenken. Stenfert Kroese (1991)
Min, R, P. Kommers, H. Vos en C. van Dijkum (1998)
Een voorstel om te komen tot een model van leren. (in Dutch; 1e concept;
gepubliceerd op Internet)
Min, R, P. Kommers, H. Vos en C. van Dijkum (1999)
A concept model for learning ... (in English; voorlopig alleen gepubliceerd op gepubliceerd op Internet)
Min, R (1999)
Een beschouwing over systemen. (1e concept; voorlopig alleen gepubliceerd op Internet)
Moonen, J., (1998)
The design and prototyping of digital learning material: some new perspectives. 1. In: Rip ........(?) en 2. In: Akker en Plomp.....











